1/√(1 x^2) 積分 330275-1/1+x^2 積分 log

May 23, 21 · 線分((1√2)/2, (1√2)/2)と線分(1/2(1√2)/2, 1/2(1√2)/2)の比Jul 28,  · 1/√ (x²2)の積分？ それなら、x=√2tanθと置換する。 （一般に、1/ (x²a²)や、1/√ (x²a²)は、x=a tanθと置換する） 計算過程は、このページでその関数を入力し（1/sqrt (x^22)と入力）、Goして、Show stepsで判る。第6 章積分技巧 62 分部積分 例 617 ∫ x x √ x21 dx 。 例 618 ∫ √ 2x23 x4 dx 。 例 619 ∫ (secxtanx)2dx 。 例 6110 ∫ ˇ 4 0 √ 1cos4xdx 。 例 6111 ∫ 1 1−cscx dx 。 例 6112 ∫ dx sinxcosx 例 6113 ∫ sin4xcos5xdx 。 例 6114 ∫ cosxcos2xcos3xdx 。 例 6115 ∫ 1 x √ lnx dx 。 例 6116 ∫ln2 0 4exsinhxdx 。 例 61

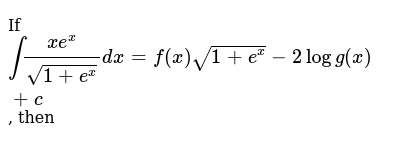
If Int Xe X Sqrt 1 E X Dx F X Sqrt 1 E X 2logg X C Then

1/1+x^2 積分 log

1/1+x^2 積分 log-くろべえ JG1BGT の受け狙い人生 >> 数学，学校，旅行，単車，鉄道，囲碁，トロンボーン，ドラム，アマチュア無線 JG1BGT，CW（モールス）, Always QRP CWJan 19, 16 · 積分公式 ∫ (x^a)dx = x^ (a1) / (a1) C （a≠1） に、1/√x =x^ (1/2) （つまり a = 1/2 ) として計算してください。 計算してみれば、 ∫ (1/√x)dx = x^ (1/2 1) / (1/2 1) C = x^ (1/2) / (1/2) C = 2*√x C です。

1 根号下 1 X平方 立方乘以dx 求定积分 雨露学习互助

Sep 08,  · 結果如下圖： 解題過程如下： 積分公式主要有如下幾類： 含axb的積分、含√（abx）的積分、含有x^2±α^2的積分、含有ax^2b（a>0）的積分、含有√（a2x^2） （a>0）的積分、含有√（a^2x^2） （a>0）的積分。一変数関数の広義積分(復習) 例 定積分Z 1 0 1 √ x dx を考える。 これを次のように計算する のはそのままでは定義に反する： Z 1 0 1 √ x dx = 2 √ x 1 0 = 2Feb 03, 21 · \(\int\frac{1}{\sqrt{x^21}}dx\)を解くのに必要な道具 置換積分 置換積分 \(関数f(x)が連続であり、関数\varphi(t)は、微分可能で導関数が\varphi'(t)\)が連続とする。このとき $$\int f(x)dx=\int f(\varphi(t))\varphi'(t)dt$$ が成り立つ。 \(\int\frac{1}{\sqrt{x^21}}dx\)の解法 \(x=tan\thetaとおくと\)

Oct 12,  · xe^{x}(1e^{2x})^{n(1/2)}0,∞などの定積分 (tan^{1}x)^2/x^2√(1x^2)0,∞などの定積分;ただし積分定数は省略して 良い (1) ∫ x2 (x3 4)32 dx (2) ∫ tanhxdx (3) ∫ 1 √ (2−x)(x−1) dx (4) ∫ ex ex −1 dx (5) ∫ sin2 xdx (6) ∫ tan2 xdx (7) ∫ sinxcosx sin2 x3sinx2 dx (8) ∫ x √ x2 2dx (9) ∫ arctanxdx (10) ∫ arcsinxdx レポート問題102 次の定積分・不定積分を求めよ (1) ∫ 1 0ガンマ関数 Γ(s) = Z ∞ 0 e−xxs−1 dx をガンマ関数という． s > 0のとき，Γ(s)が収束する．それを示すためにf(x) = e−xxs−1 とおく． (1) 任意のaについて区間(0,aでxs−1 はf(x)の優関数であるので，f(x)が積分可能である． (2) lim x→∞ f(x) e−x/2 = lim x→∞ xs−1 ex/2 = 0 より，x > a ならばf(x) ≤ e−x/2

1 次の不定積分を求めよ。 (1) ∫ logx (1x)2 dx (2) ∫ 1 (x2 1)2 dx (3) ∫ 1 x p x2 1 dx (4) ∫ sin 1 xdx 2 sinht = et e t 2 を双曲線正弦関数という。 (1) x = sinht とおくとき、t をx で表せ。 (2) x = sinht と置換することにより、 ∫ 1 p x2 1 dx を求めよ。 また、 ∫ p x2 1 dx をSep 21, 19 · 積分では sin ⁡ 2 \sin^2 sin2 とか cos ⁡ 2 \cos^2 cos2 がきたら半角の公式だから、ここはすぐに反応できるようにね。 半角の公式 cos ⁡ 2 x = 1 cos ⁡ 2 x 2 \displaystyle \cos^2 x=\frac {1\cos 2x} {2} cos2 x = 21cos2xConsider, for example, the function 1/((x 1) √ x) integrated from 0 to ∞ (shown right) At the lower bound, as x goes to 0 the function goes to ∞, and the upper bound is itself ∞, though the function goes to 0 Thus this is a doubly improper integral Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result

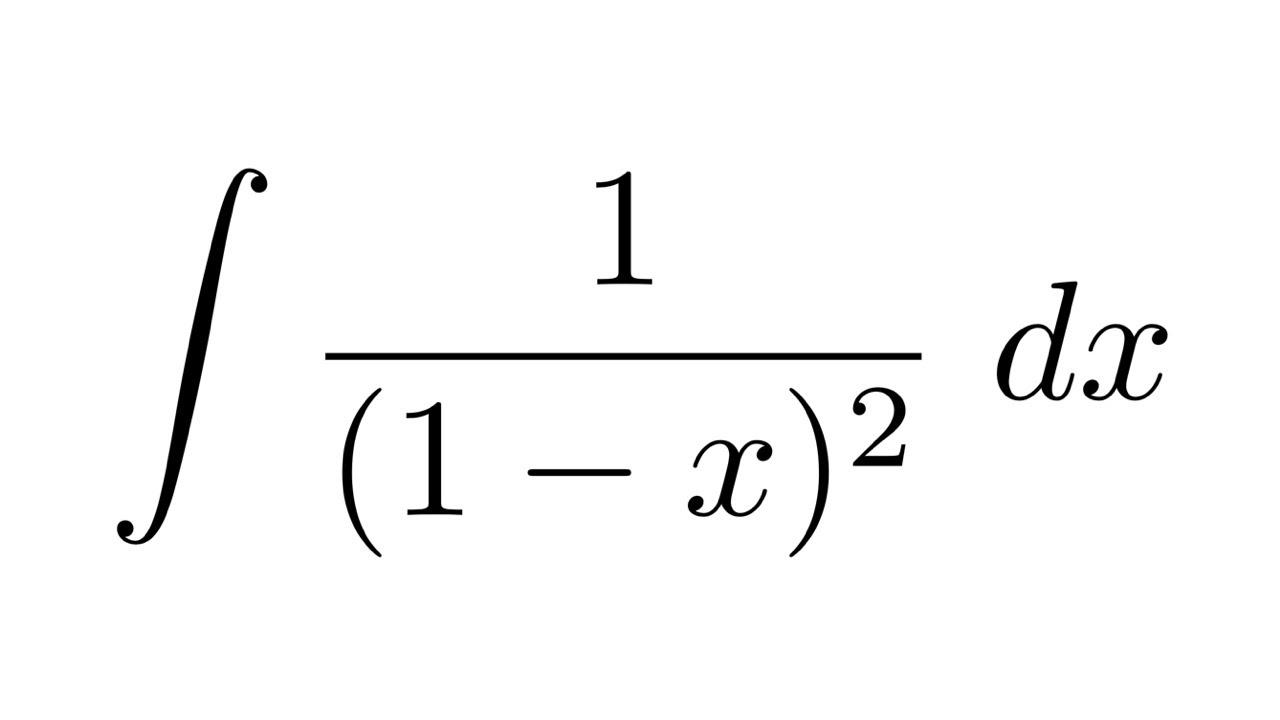
Integral Of 1 1 X 2 Youtube

求不定积分 Xarctanx 1 X 2 Dx 雨露学习互助

となりました．確かに の微分が被積分関数になっていますね． まとめ 覚えやすいように，他の積分と比較できるようにまとめておきます．いきなり書きますが，良い練習問題になると思います．まずは，右辺を に等しいと置いて， を求めるのです．ちなみに としておきます．Start studying 積分 Learn vocabulary, terms, and more with flashcards, games, and other study toolsX = 1 √25 In Math, i is called the imaginary unit It satisfies i 2 =1 Both i and i are the square roots of 1 Since a square root has two values, one positive and the other negative x 2 2x 26 = 0 has two solutions x = 1 √ 25 • i or x = 1 √ 25 • i Solve Quadratic Equation using the Quadratic Formula

Evaluate Cosx 1 Ex Dx X P 2 P 2 Sarthaks Econnect Largest Online Education Community

Integral Wikiwand

Jul 28, 19 · 1/√(a^2x^2)の積分について(a≠0) 答えはSin^(1)x/aですがこのaの絶対値は必要なのでしょうか。仮に絶対値がなかったらどうなるのでしょうか。インターネットのサイトで調べたと1 √ 1 − x2 dx = sin−1 x C 証明 • 1 − x2 > 0 より，−1 < x < 1 である． • そこで，x = sin t として置換積分をする． • dx dt = (sin t)′ = cos t より，dx = cos tdt． • −1 < sin t < 1 より， sin t を − π 2 < t < π 2 で定義された関数と考える． （このとき，cos t > 0 である） (10/14)May 18,  · この記事では、特定の 1/√1x^2の積分 について 置換積分を2回 行う方法で解説します。 また、 置換積分を1回でのみ解ける簡略的な方法 についても解説しています。 最後には、例題もありますので、例題を見ながら理解していただくのもおすすめです

Gaussian Integral Wikipedia

不定积分x E 1 Dx 计算不定积分 E的1 X次方 X平方dx

Sep 08,  · 那麼湊微分即可 原積分=∫05√ (1x²)d (1x²)=1/3 * (1x²)^ (3/2)C，c為常數如果是∫√ (1x²)dx，使用三角代換 而你圖片上的題目已經解答的很清楚 11 根號下x^2可以分解變成根號下（X1）乘（X1），同樣根號下1X^2也可以分解成根號下（X1）乘（1X），因為X1(1) (sin−1 x)′ = 1 √ 1−x2, (2) (cos−1 x)′ = − 1 √ 1−x2, (3) (tan−1 x)′ = 1 1x2 対応する不定積分の公式は次のようになる。 公式 (1) ∫ dx √ 1−x2 = sin−1 x C, (2) ∫ dx 1x2 = tan−1 x C 小谷健司 微分積分I 第6 回1Jun 30, 09 · 教育用の覚書。 置換 積分 を用いて解く。 √x2 a2 = t − x とおいて t の 積分 に書き換える *1 *2 。 この置き換えでは tをxの式で表すと t = x √x2 a2 xをtの式で表すと x = t2 − a2 2t ↑この式よりdxの変換は dx = t2 a2 2t2 dt √x2 a2 をtの式で表すと √x2 a2 = t2 a2 2t これらを代入してxの式をtの式に書き換える。

Improper Integral Wikipedia

求 1 X与1 X的商的不定积分 搜狗指南

Dec 03, 11 · 正しい積分範囲で積分すれば発散しませんよ。 I=∬D 1/√(1xy) dxdy =∫0,1{∫0,x 1/√(1xy) dy}dx =∫0,1{(2/x)√(1xy)y0,x}dx =∫0,1 (2/x){1√(1x^2)}dx = limx→122√(1x^2)2log{1√(1x^2)} 22√(1x^2)2log{1√(1x^2)}(x=0) = 2(222log2) = 22log2から, 答えはlogx2=2 (5) arcsinx の微分は1= √ 1−x2 であるので, 部分積分すると, ∫ arcsinxdx = xarcsinx− ∫ x √ 1−x2 dx = xarcsinx √ 1−x2 例題17 次の関数を積分せよ (1) exsinx, (2) 1 (x2 a)n (a̸= 0 ,n̸= 1) 略解例(1) は高校でよくやっているだろう (2) も同じ考えで1−x2 dx 解 部分積分法により, I = ∫ (x)′ √ 1−x2 dx = x √ 1−x2− ∫ (− x2 √ 1−x2) dx = x √ 1−x2 ∫ x2 √ 1−x2 dx となる 右辺の不定積分の項を計算すると, ∫ x2 √ 1−x2 dx = ∫ −(1−x2)1 √ 1−x2 dx = − ∫ √ 1−x2 dx ∫ 1 √ 1−x2 dx = −I sin−1 xC したがって整理すると, I = x √ 1−x2 sin−1 x 2 C (10) I = ∫ √ x2 1dx 解 部分積分法により, I = ∫ (x)′

實用特殊積分求法 每日頭條

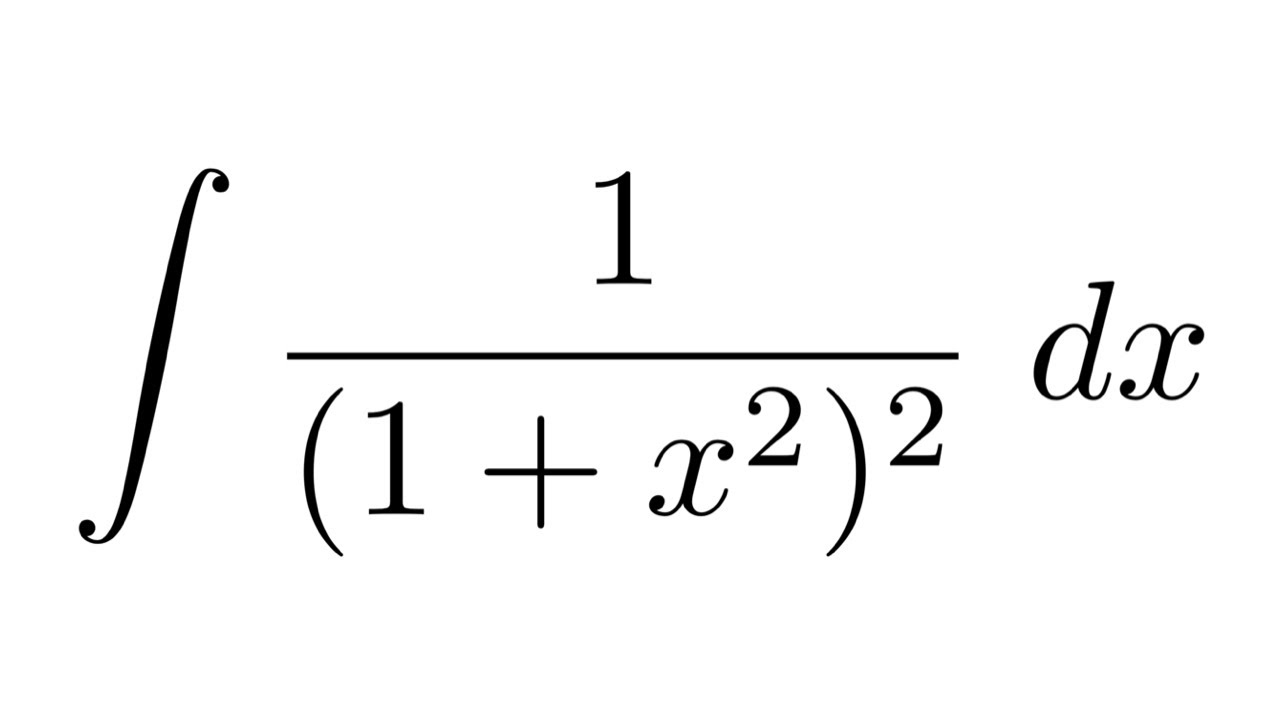
Integral Of 1 1 X 2 2 Substitution Youtube

Apr 03, 18 · 上野竜生です。√(x 2 a 2)の積分を丁寧に解説しようとすると長くなったのでラスボス前の中ボス程度の1/√(x 2 a 2)は別ページにわけることにしました。 ラスボスについてはこちらをご覧ください。 今回考える積分May 13, 21 · 演習 (1) 予定 (1) データ解析学 (18) 数式処理 (1) (30) moriokau (19) 情報処理演習 (18) 生物統計 (1) oribe (2) 放送大学 (1) 18 (9) 19 (25) 面接講義 (1) 積分 (7)（C は積分定数） 112 n = 2 I2 = Z 1 x2 1 dx = arctanx C (13) x 1− 1 6 ln x2 − x 1 1 √ 3 arctan 2x

Ex 7 4 2 Integrate 1 Root 1 4x2 Class 12 Ncert Ex 7 4

Contour Integration Wikipedia

May 25,  · その中でも計算が必要なのは、積分の部分だけなので、 ∫ 1 √x2 1dx この積分を解けばいいことになります。 ただこの式の計算は、結構大変なので別ページにあります。 積分1/√1x^2の積分、1/ax^2の積分、2回の置換を行う この記事では、特定の1/√1x^2の積分について置換積分を2回行う方法で解説します。 また、置換積分を1回でのみ解ける簡略的な方法に1 √ xln xdx (b) Z ln(√ x 1)dx (c) Z cos(lnx)dx (a) íl根Wúb函bí4", ªøŸ˜Z寫A 1 2 Z4 1 √ xlnxdx QO根W累 í%ð (2), I u = lnx ⇒ du = 1 x dx dv = √ xdx ⇒ v = 2 3 x3/2 12 2×bç系PM1 1 View solution steps Steps Using Derivative Rule for Sum \frac { { x }^ { 2 } } { x1 } \frac { 1 } { 1x } x − 1 x 2 1 − x 1 To add or subtract expressions, expand them to make their denominators the same Least common multiple of x1 and 1x is x1 Multiply \frac {1} {1x} times \frac {1} {1}

Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C

How Come You Halve The Integral Of 2x 1 2 Dx Quora

1 √ x2 1 − a x 2)dx =ln p x2 1 = x−1 (積分因子有算出來得5 分，有錯整題最多給2 分。) on both sides of the differential equation and get 1 x yJan 12,  · この積分定数氏は普段色々な方を批判してるけど，この人は逆に，頭いいのか疑問です．出身大学はどこなんでしょうか？ (学歴が全てとは思いませんが，教育の批判を，する方なので一つの目安です．) あと，この人の批判は納得することも多いんです平成15年5月25日 流れ星 第119回 数学的な応募問題解答 ＜解答募集期間：5月6日～5月25日＞ 複雑な不定積分 NO1「 toru 」さん 5/06 14時12分 受信更新5/25 問題1 x= tanθ (π/2 ≦ θ ≦ π/2) とすると dx =1/(cosθ)^2, 1/(1x^2)=(cosθ)^2

求不定积分 X 2 9 1 2 Dx X 雨露学习互助

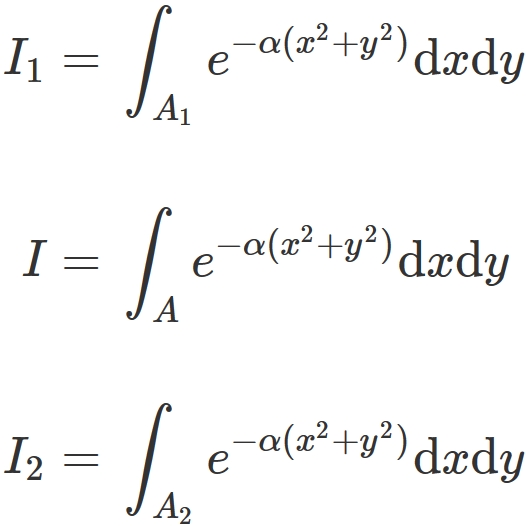
Gaussian Integral Formula And Proof Semath Info

広義積分 例 定積分Z 1 0 1 √ x dx を考える。 これを次のように計算する のはそのままでは定義に反する： Z 1 0 1 √ x dx = 2 √ x 1 0 = 2 理由Z 1 0 1 √ x dx を定義する為のRiemann 和は発散し得る： −1 k=0 1 n 1∫0,π(1/√(sin x))dx この広義積分の収束と発散を判定せよという問題なのですが解放を教えてください。 現在講義で習ったのが f(x)a,b)で連続 ョμ≧1 lim(x→b0) (bx)^μ*f(x)が収束 ならば ∫a,bf(x)dxは発散 という内容なのでこれをうまく利用するみたいですが、まったく解法が浮かびませ1 √ a2 −x2 Arcsin x a a > 0 1 x2 a2 1 a Arctan x a a > 0 1 練習34 （教科書p91 問39）次の定積分を求めよ。 (1) ∫ 1 0 x 1x 2 dx (2)

对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园

Ex 7 4 24 Integration Dx X 2 2x 2 Equals A X Tan 1 X 1

公式（積分）‐ 6 ‐ いろいろな積分（積分定数C は省略） 三角関数 ∫ sinx dx = cosx ∫ cosx dx = sinx ∫ sin2 x dx = ∫ 1 cos2x 2 dx = x 2 sin2x 4 ∫ cos2 x dx = ∫ 1 cos2x 2 dx = x 2 sin2x 4 ∫ sin3 x dx = ∫Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history逆三角関数の導関数 逆正弦関数y = sin−1 x の導関数を考える。 −1 < x < 1 の範囲で考えると, 値域は−π/2 < y < π/2 です。 だ から, cosy > 0 です。x = siny なので, 逆関数の微分の公式より, dy dx = 1 dx dy = 1 cosy 1 √ 1−sin2 y 1 √ 1−x2 したがって, (sin−1 x)′ = 1 √ 1−x2 π/2 −π/2 小谷健司 微分積分演

6 2 6 1 瑕積分int 0 4 1 X 1 1 3 Dx Youtube

How Do You Find The Antiderivative Of Int Sqrt 9 4x 2 Dx Socratic

Sep 10, 16 · 積分定数氏の想定する生徒は「塾に通おうとする勉強に対して熱意のある生徒」であり、授業は高々5,6人に少人数クラスを想定してるんだろう。 104 132人目の素数さん (水) IDpsfauyQ/5−4x−x2 dx 問題13 次の不定積分を求めよ (1) ∫ (4x3) 4dx (2) ∫ x (x5 3)6 dx (3) ∫ 1 (2x5)4 dx (4) ∫ 2x2 x2 2x4 dx (5) ∫ √ 4x1dx (6) ∫ 8x3 √ 2x4 3 dx (7) ∫ 1 √ 3−2x−x2 dx (8) ∫ sin3 xdx (9) ∫ sinx 2cosx dx (10) ∫ sec2 x 2tanx dx (11) ∫ cotxdx (12) ∫ x2ex3 dx (13) ∫ (ex 1)3ex dx3 置換積分をすることにより, 次の積分を計算せよ (1) I1 = Z (5x−2) √ 1− xdx (2) I2 = Z x(x2 3)5dx (3) I 3 = Z cos3 xdx (4) I 4 = Z sin2 xcosxdx 解答例以下, C は積分定数とする (1) √ 1− x = t とおくと, x = 1−t2 より, dx dt = −2tよって, I1 = Z {5(1−t2)−2}t·(−2t)dt = Z

How To Integrate 1 Sqrt X 2 1 Youtube

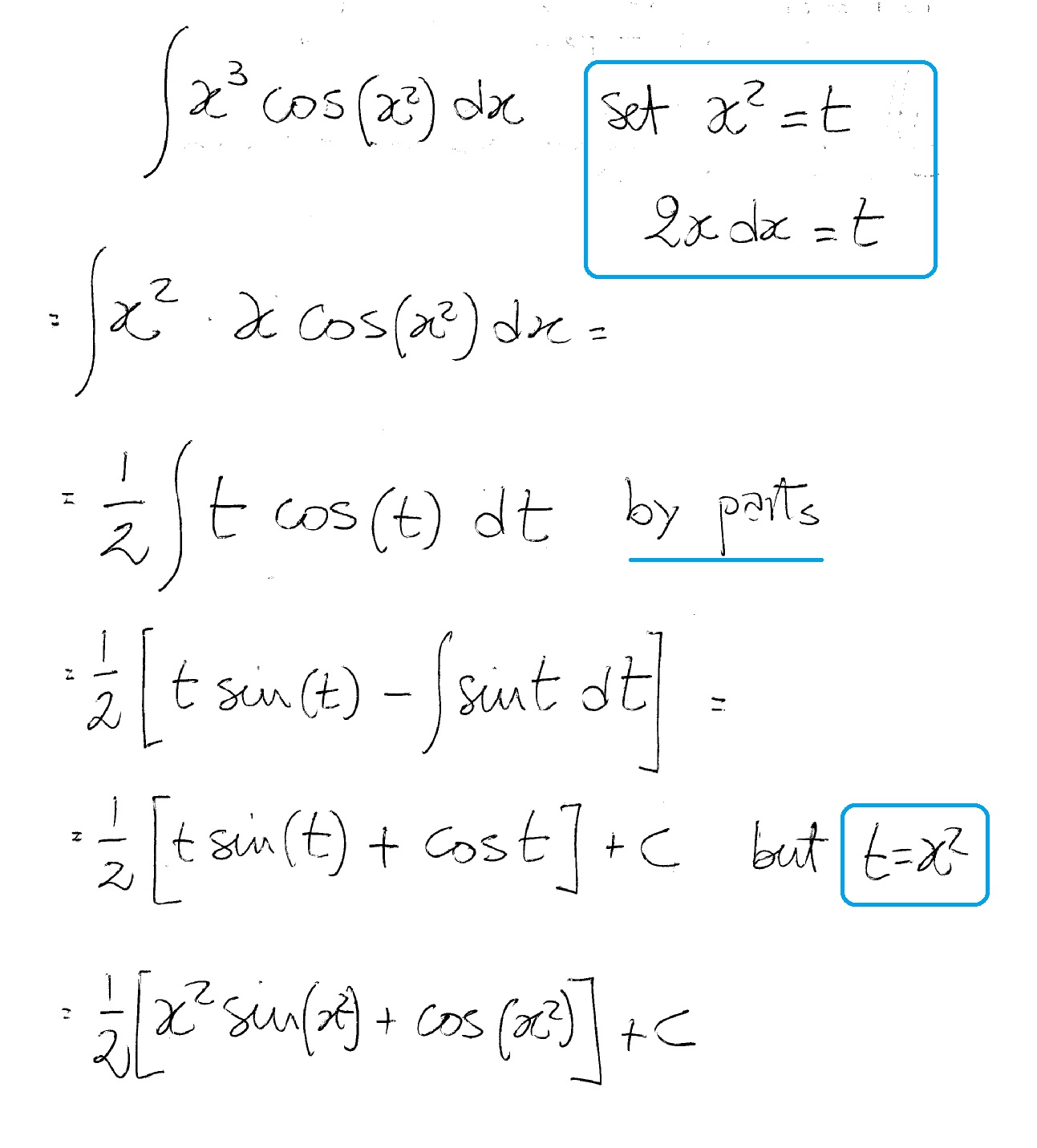
How Do You Integrate X 3cos X 2 Dx Socratic

積分 x^2*√ (x^21) このように，左辺と同じ積分 ∫ x2√x21dx ∫ x 2 x 2 1 d x が右辺にも現れた．Jan 14, 21 · x√(1x^2)の積分を教えてください 答えは1/3(1x^2)^3/2です 大学数学 ∫x^3/x^21の積分が分かりません、どのように解くのでしょうか 数学 数3 積分ただし, 積分定数はC とせよ (1) I = ∫ xex2 dx (2) I = ∫ sinxcos4 xdx (3) I = ∫ logx x dx (4) I = ∫ x √ 1−x2 dx (5) I = ∫ x x2 1 dx (6) I = ∫ cosx sin2 x1 dx (7) I = ∫ 1 x2 2x5 dx (8) I = ∫ 1 √ −x2 2x3 dx (9) I = ∫ √ 1−x2 dx (10) I = ∫ 1 √ x2 1 dx 2 部分積分法を使って次の不定積分

1 根号下 1 X平方 立方乘以dx 求定积分 雨露学习互助

What Is The Integral Of Dx Sqrt X X 2 Quora

X2 A t, 1 √ x2 A dx = 1 t dt Z 1 √ x2 A dx = Z 1 t dt = logt = logx p x2 A 3－4 不定積分 Z p x2 Adx を求めよ。 34解答 √ x 2A = t−x とおくと、x A = t2 −2txx ,A = t2 −2tx 両辺をt で微分すると、0 = 2t−2x−2t dx dt 、 dx dt = t−x t = √ x2 A t, 1 √ x2 A dx = 1 t dt p x2 A = t−x = tè ∫ √(1 x 2 )2xdx = ∫ √u du = 2/3 u 3/2 C = 2/3 (1x 2) 3/2 C 計算積分的微分時，要先看積分的下限是否是常數，若不是就先換，換完後，確認積分的上限是否和 dt 一樣，不一樣就假設 u= 上限再算

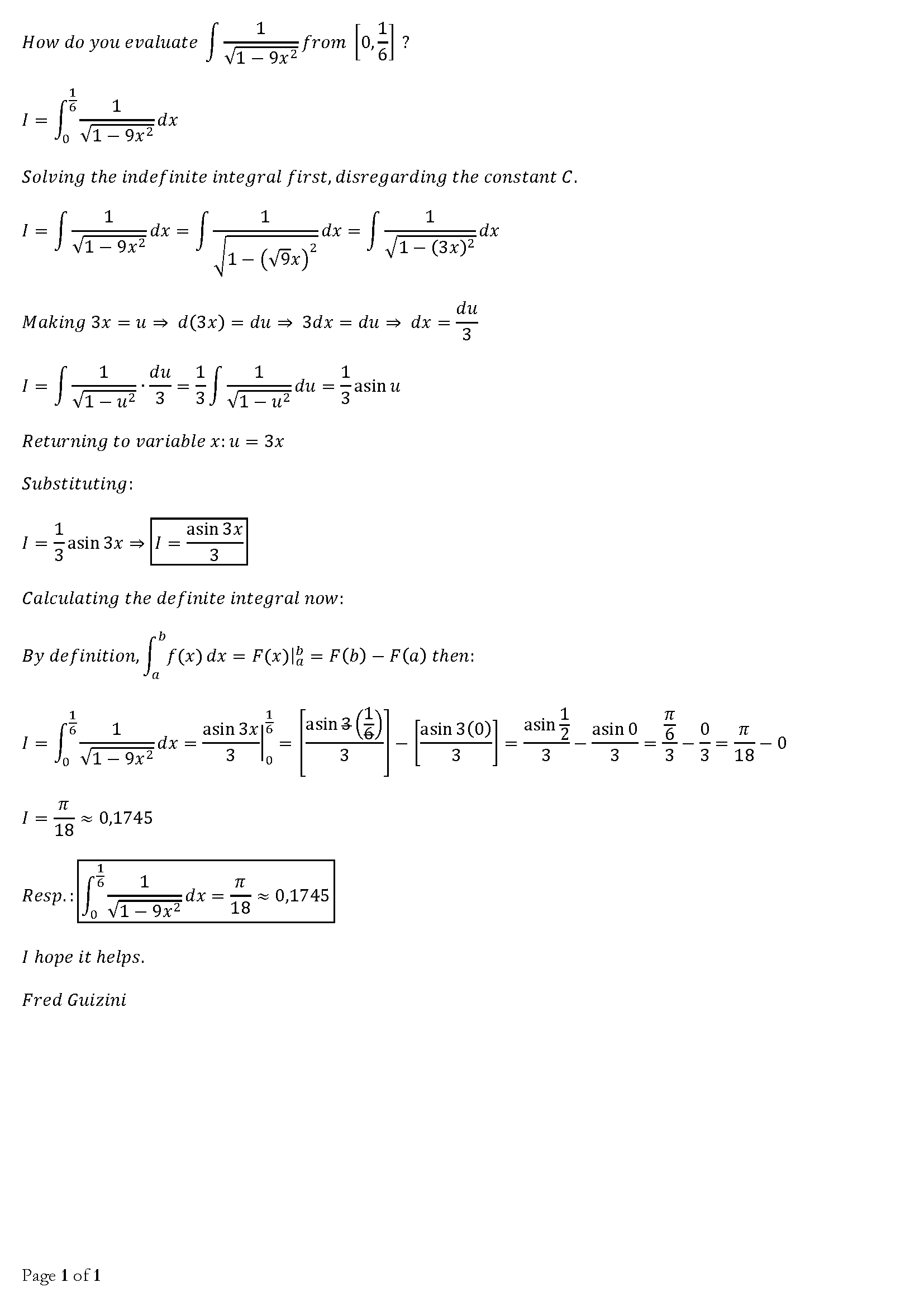
How Do You Evaluate Int1 Sqrt 1 9x 2 Dx From 0 1 6 Socratic

高数求定积分0到1 Ln 1 1 X 2 Dx咋做呀 作业 慧海网

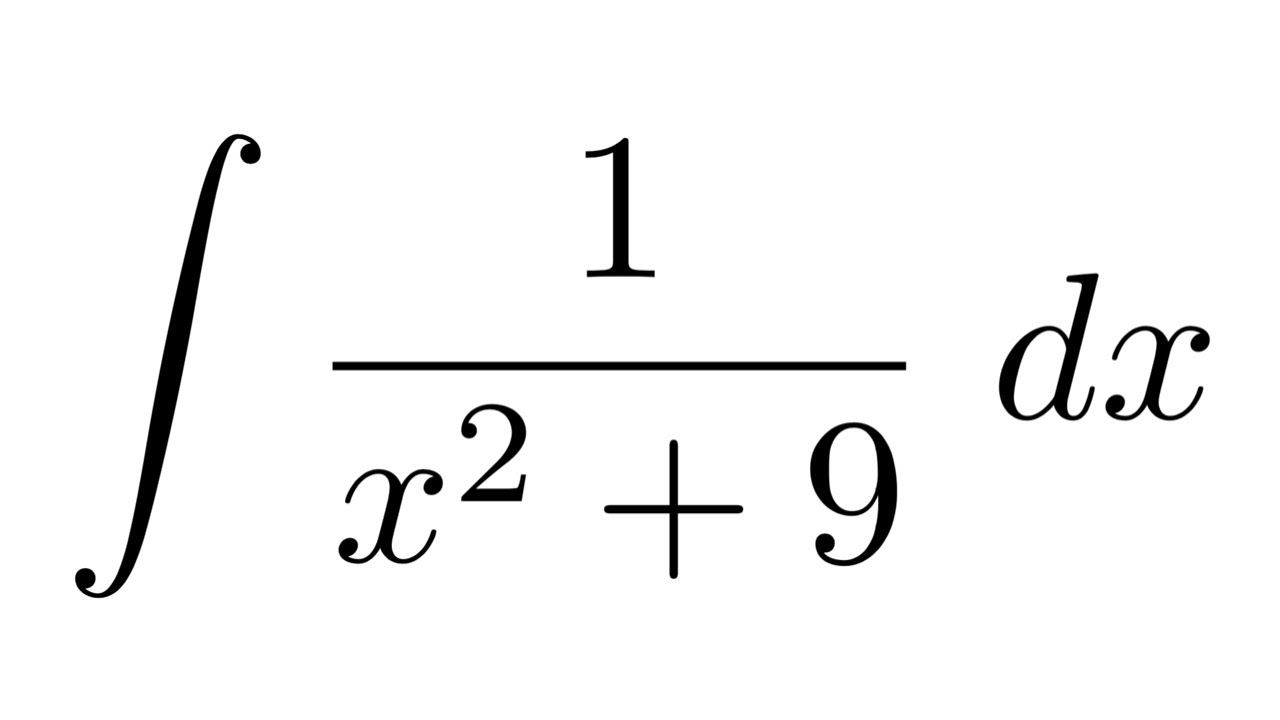
Integral Of 1 X 2 9 Substitution Youtube

Int 2 2 X 3cos X 2 1 2 Sqrt 4 X 2 Dx

置換積分の方法 置換方法を覚えておきべき積分問題 大学入試数学の考え方と解法

求定积分 上限根号3 下限0 X乘根号下1 X 2 Dx 雨露学习互助

不定积分 X 2 1 X 4 1 Dx计算具体过程 雨露学习互助

对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园

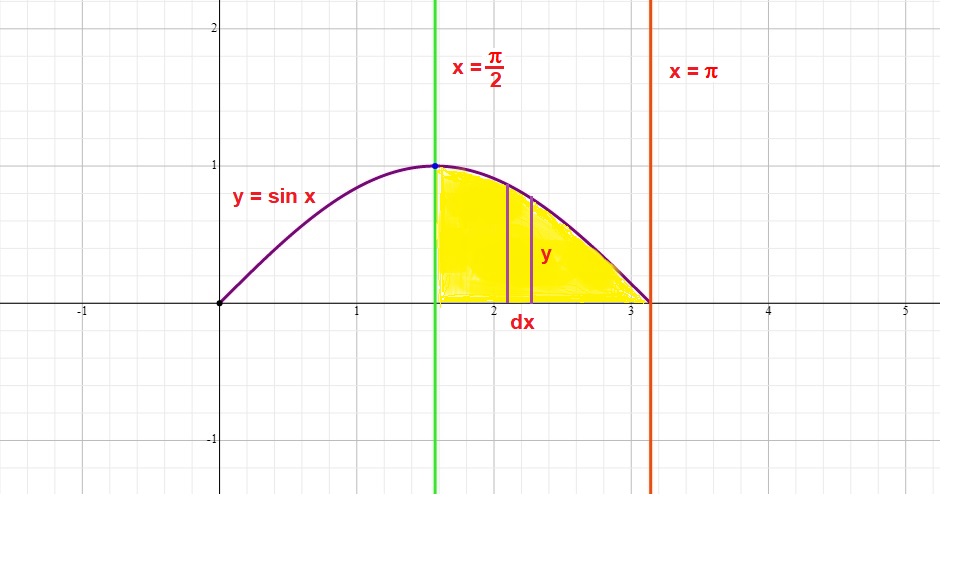
Integral Int Dx X 2sqrt X 2 16 Socratic

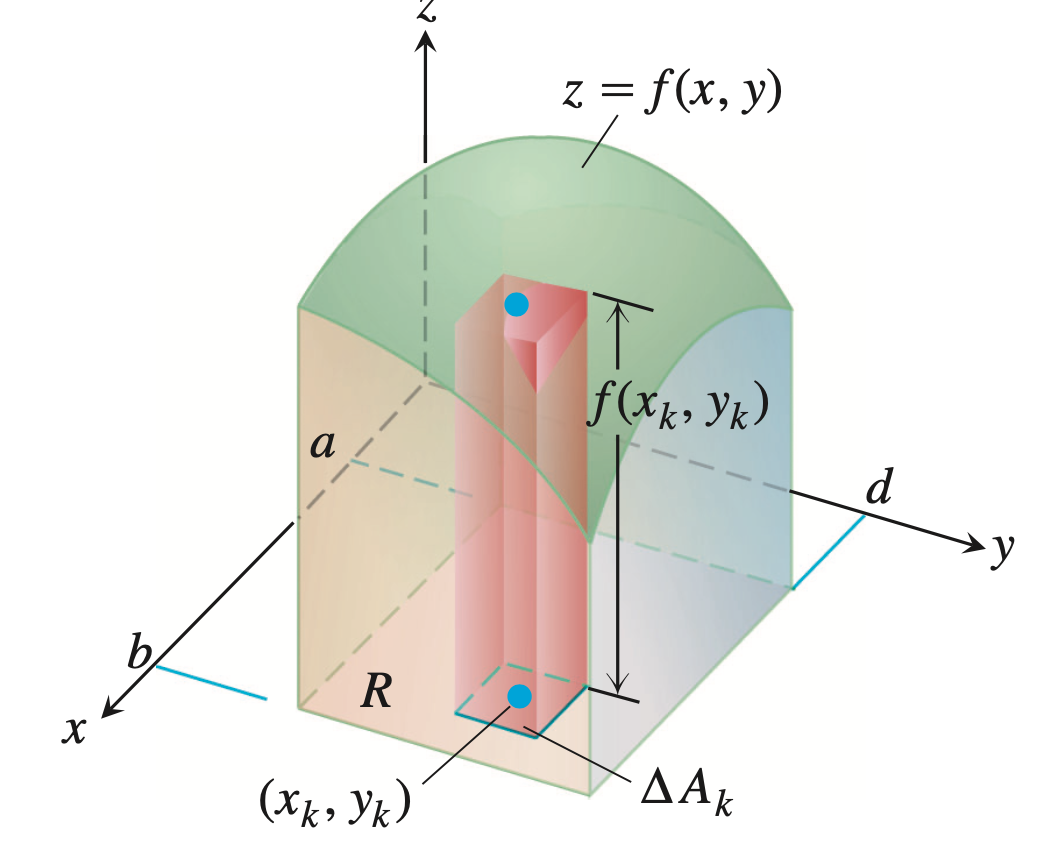
重积分 Guoning Wu Ph D

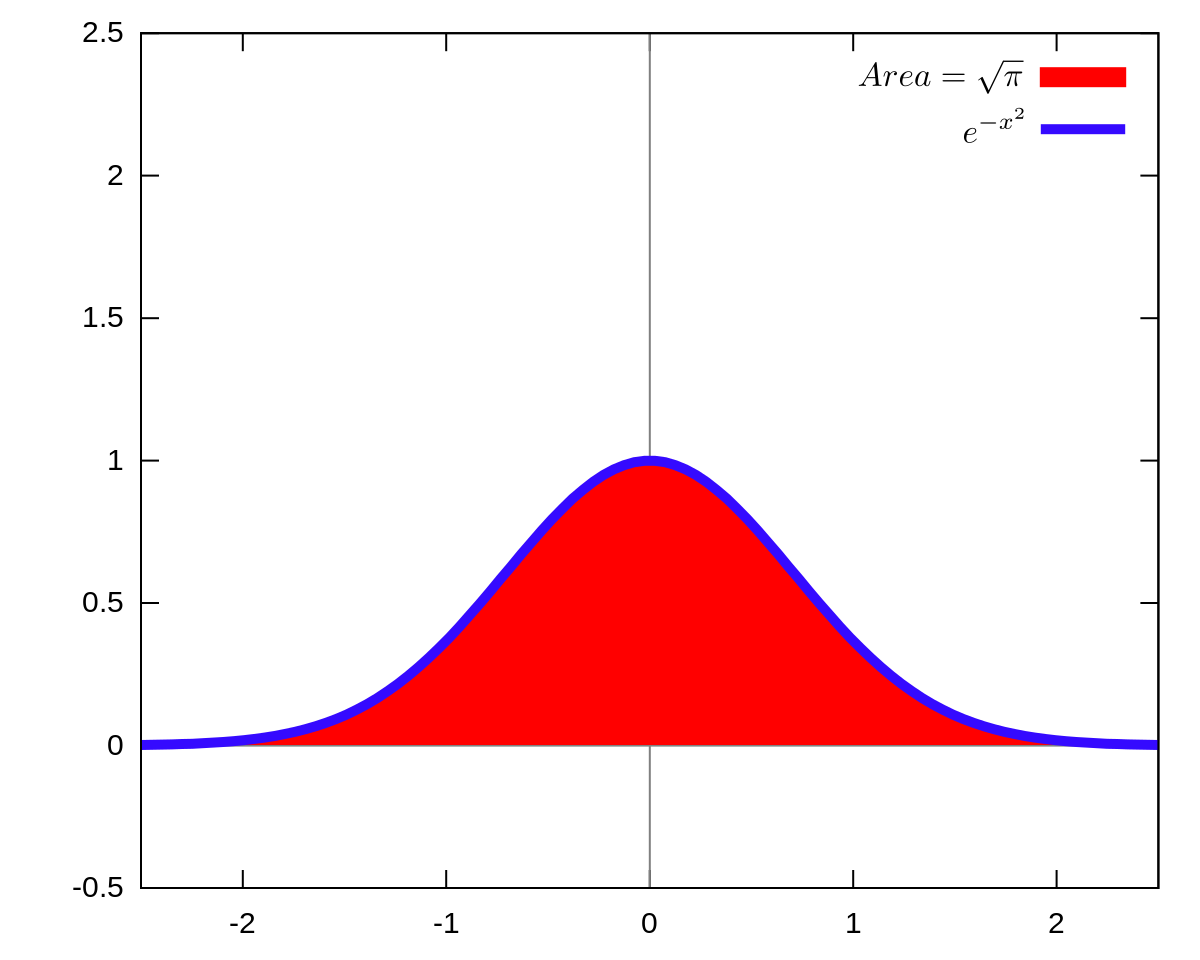
Gaussian Integral Wikipedia

求不定积分 1 二次根号下 E的x次方加二 雨露学习互助

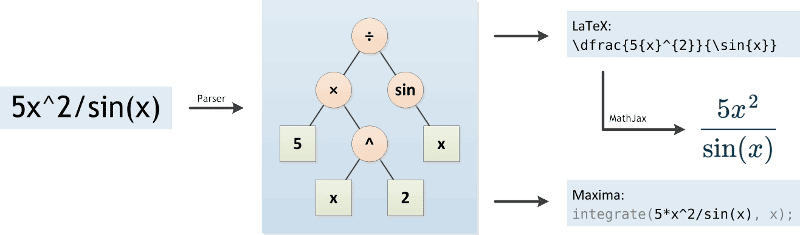
Integral Calculator With Steps

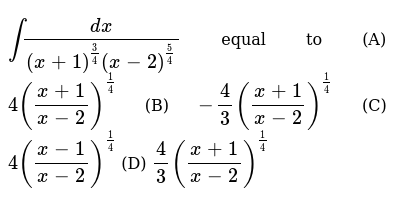
Int Dx X 1 3 4 X 2 5 4 Equal To A 4 X 1 X 2

Integral Xsinx 1 Cos 2 X Dx I Get That In Walfram Www Wolframalpha Com Input I Integral Xsinx 2f 281 2bcos 2x 29 But It Does Not Help Enotes Com

Evaluating Int Sqrt 1 T 2 Dt Mathematics Stack Exchange

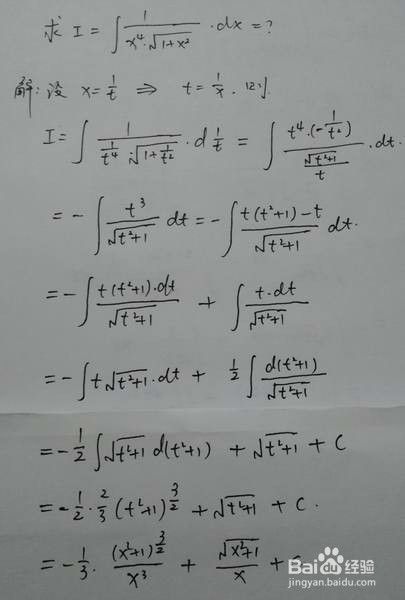
两种方法求x 4 1 X 2 的倒数的不定积分 百度经验

What Is The Integral Of Math Sqrt Tan X Math Quora

求不定积分 1 X Dx 根号下 1减x的平方 数学解答 作业小助手

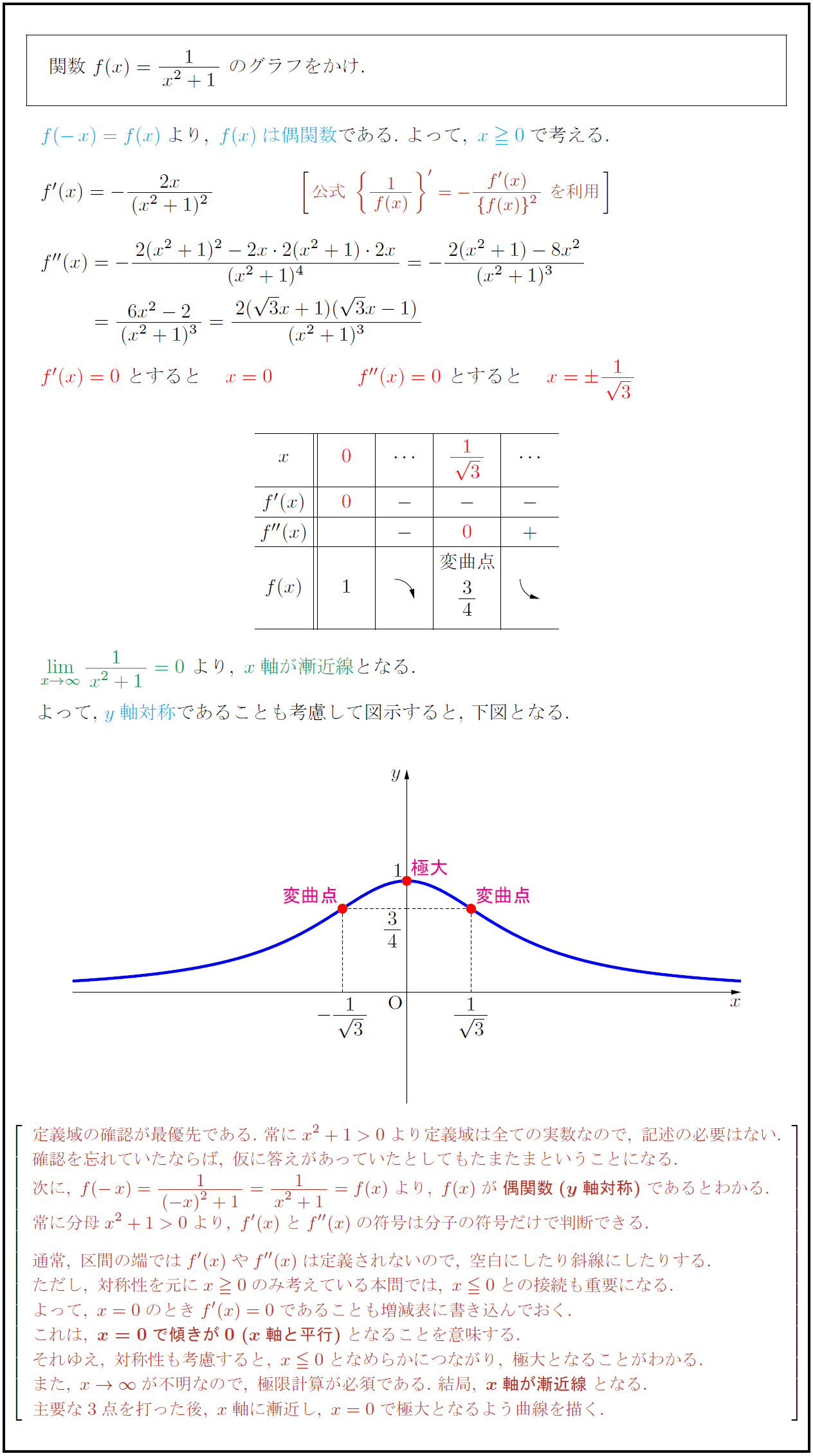
高校数学 分数関数 Y 1 X 1 のグラフ 受験の月

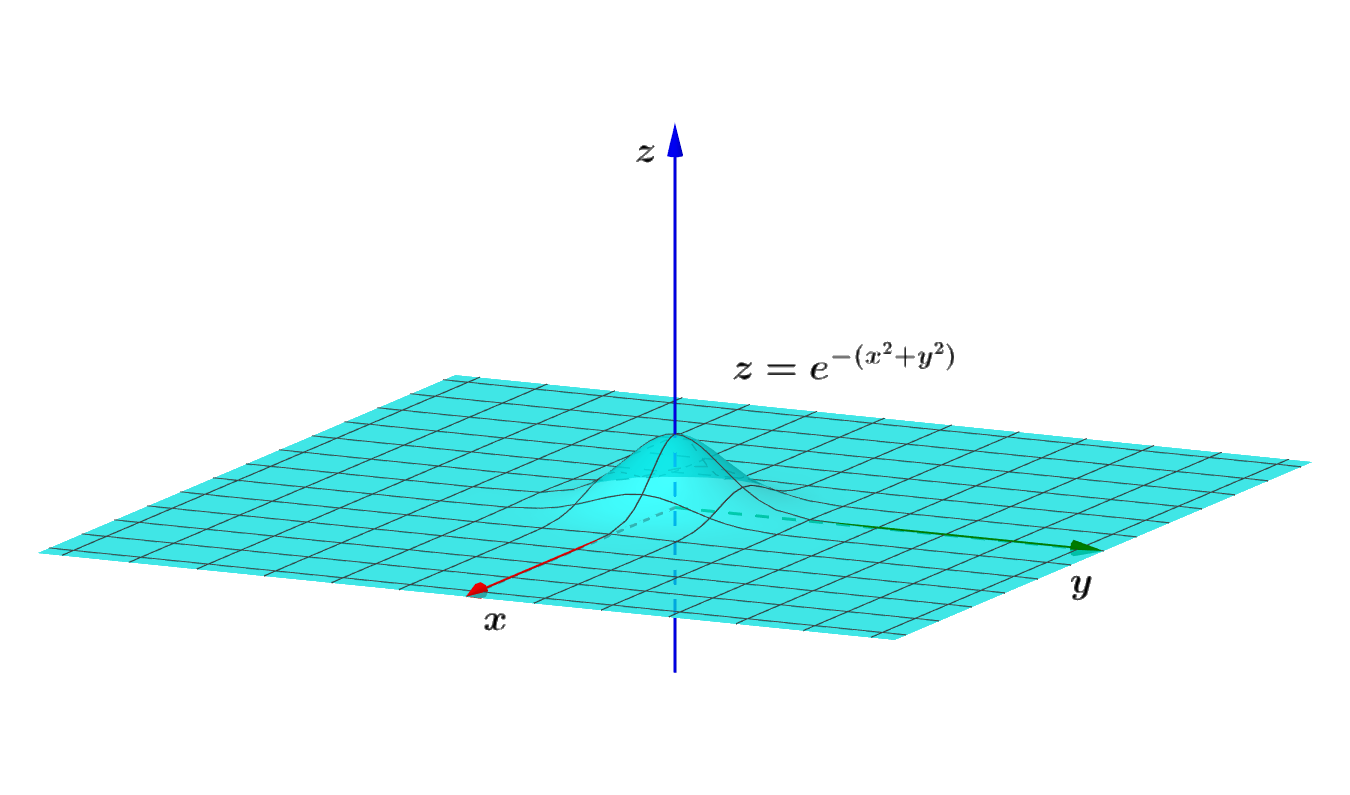
无穷积分 E X 2 Dx 的几种巧妙解法 Blogs Of Zcy1221 Csdn博客

定积分证明 Dx 1 X 2 X 0 在 X 1 和在 1 1 X 的定积分相等 作业 慧海网

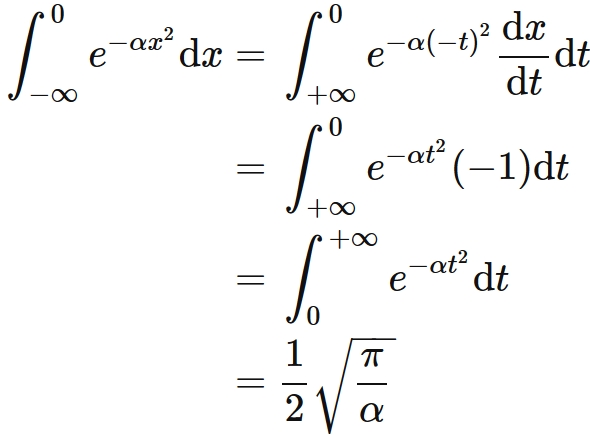
Gaussian Integral Formula And Proof Semath Info

1 X 2 A 2 Dxの計算 物理のかぎしっぽ

Integral Of 1 Sqrt 1 X 2 Substitution Youtube

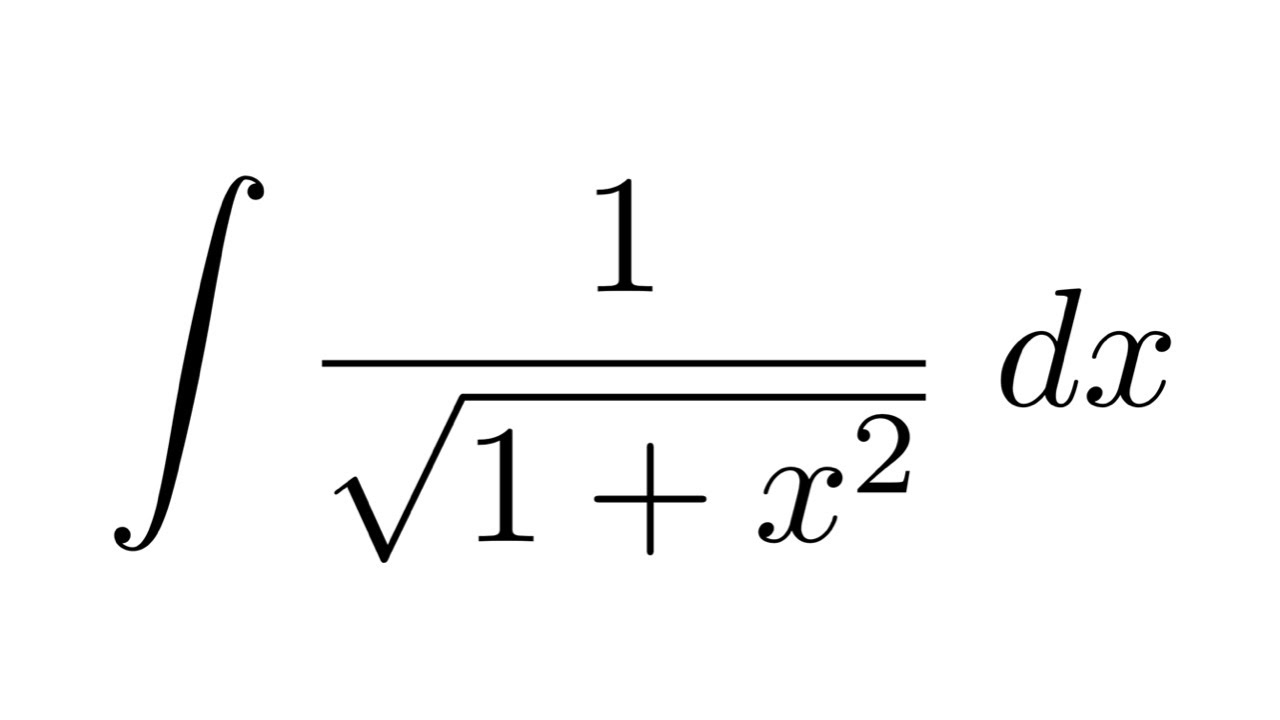
Integral Of 1 Sqrt 1 X 2 Substitution Substitution Youtube

知識家 單元16 5 代換積分 X 1 X Dx A 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目 隨意窩xuite日誌

X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx

求2道积分的1 1 X 根号1 X 2 Dx 2 X 2 4 Xdx 雨露学习互助

对于似1 1 X 4 型的不定积分的总结 Erasernut 博客园

Evaluate The Integral Of 1 X2 Stumbling Robot

标准部分分式的不定积分 Arctanx的不定积分积分 三人行教育网 Www 3rxing Org

1 X 29 X 2 Dx2 X 2 1 急 不确定积分 多次操作 详细过程 好加点o 365bet送彩金 365注单审核不能提款

Evaluate The Integral Of 1 A Bx2 Stumbling Robot

超越函数e X 2 的定积分 Norstc的博客 Csdn博客

How To Calculate Integral Of X 1 X Dx By Part Quora

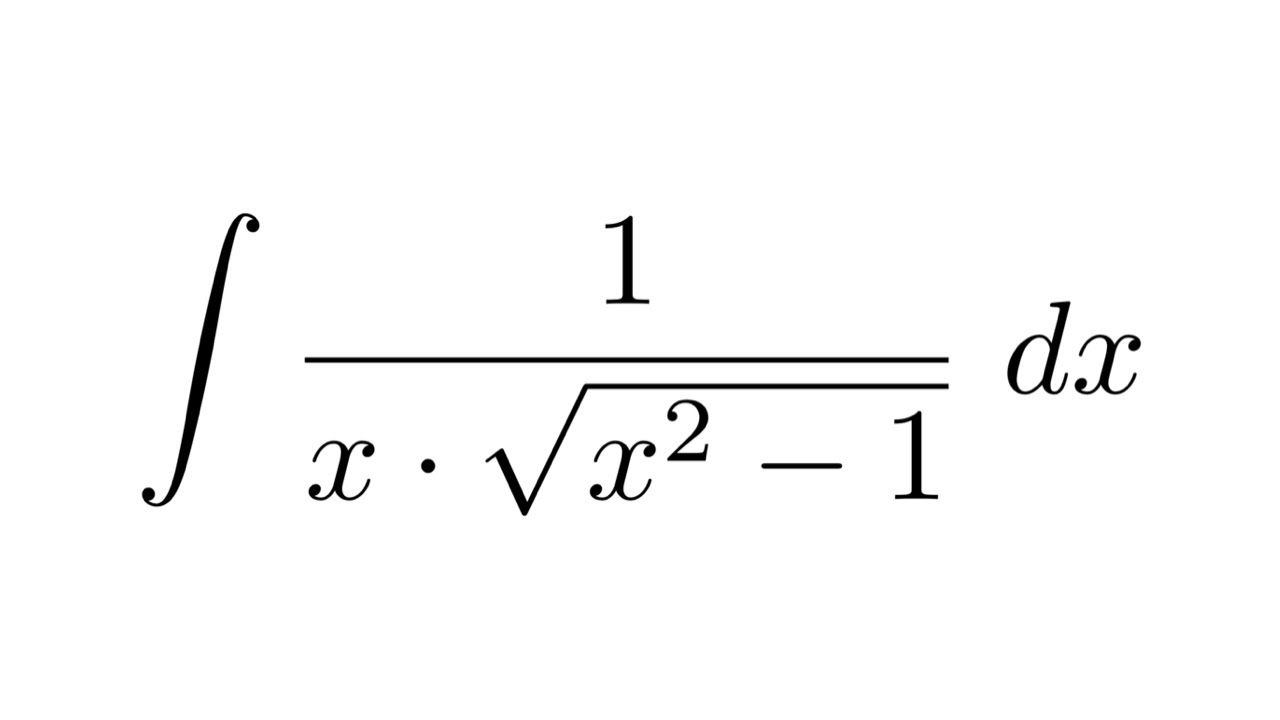
Method 1 Integral Of 1 X Sqrt X 2 1 Substitution Youtube

How To Integrate X 3cosx 2 1 2 Sqrt 4 X 2 Dx For The Interval Of 2 And 2 Quora

无法求不定积分怎么求定积分 怎么求arcsinx的不定积分 三人行教育网 Www 3rxing Org

X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx

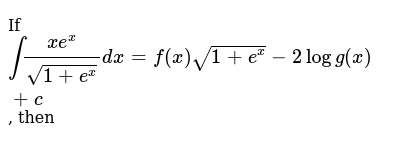
If Int Xe X Sqrt 1 E X Dx F X Sqrt 1 E X 2logg X C Then

Integral Of X 2 Sqrt 1 X 2 Substitution Youtube

How To Solve The Integral Of X 3 1 X 2 3 Quora

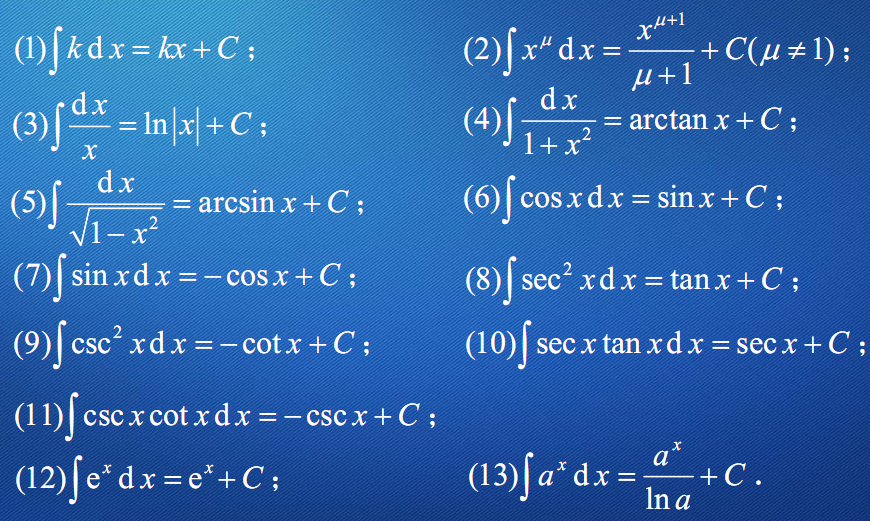
4 2不定积分的性质与基本积分表 早做准备

How Do You Integrate 1 X 2 Sqrt 1 X 2 Socratic

What Is The Integration Of 1 Xe X Quora

X2 1 X4 1求不定积分 不定积分 X4 1 X2 1 Dx

二重积分计算计算二重积分 领域开拓网

求不定积分xe X 1 X 2 Dx 雨露学习互助

X平方乘根号下x平方加1 求微分根号下x的平方加一求

What Is The Integral Of 1 1 X 2 Quora

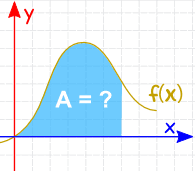
Integration Rules

X 2 1 4x 2 Dx怎么积分 微思作业本

Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C

What Is The Integral Of 2x 2 2x X 2 Quora

1 X的平方的不定积分 搜狗搜索

How To Integrate 1 X 2 3 2 Quora

Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C

怎么解这个不定积分 X 5 X 3 1 X 3 X 2 X 1 Dx 雨露学习互助

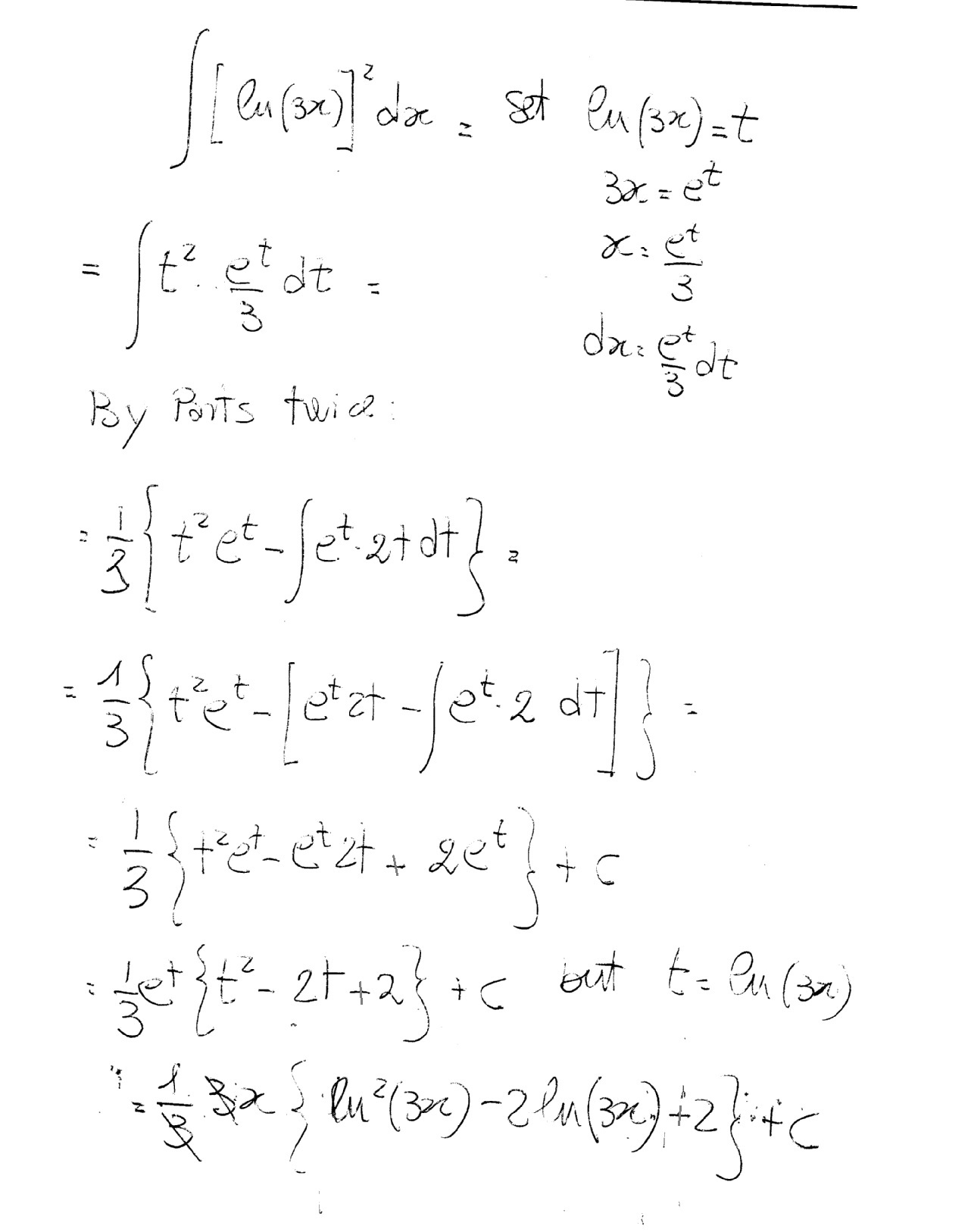
How Do You Find The Integral Ln 3x 2dx Socratic

积分公式和常用方法总结 Leemboy的博客 Csdn博客 积分公式

1 X 2 1 積分5 Lnzikz

二重积分的积分区域怎么确定的 二重积分的积分上下限如何确定 比如积分区域x 0 1 Y 0 1 有的时候y的上 三人行教育网 Www 3rxing Org

用坐标系计算二重积分 D 根号 1 X 2 Y 2 Dxdy D X 2 Y 2 1 X 0 Y 0 雨露学习互助

E的x次方定积分x乘以e的负x次方 定积分

高数不定积分求解 Ln 4 X 2 Dx 雨露学习互助

1 X 1 Dx积分从1到3 作业 慧海网

X 3 X 2 1 の不定積分 申し訳ありませんが 画像を作成しましたの 数学 教えて Goo

计算下列各定积分f 0 2 绝对值 1 X Dx F 0 P 4 Tan Xdx 雨露学习互助

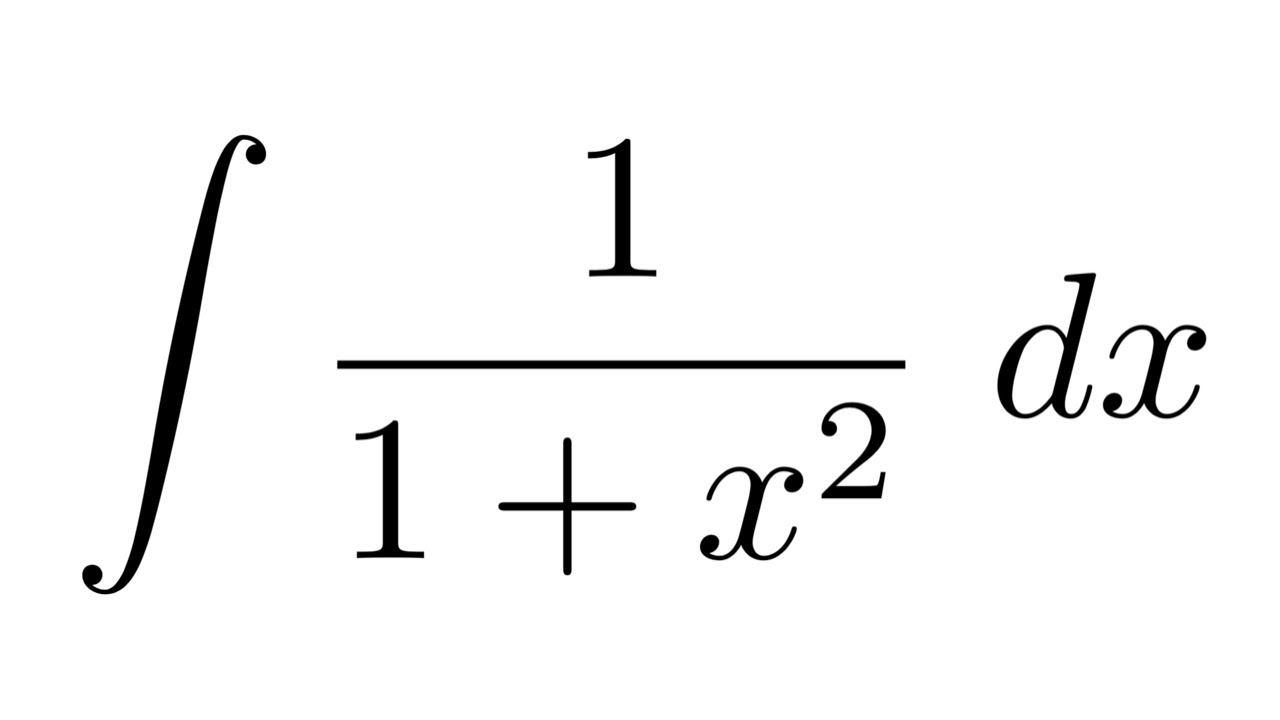
Integral Of 1 1 X 2 Substitution Youtube

不定积分x 3 Sqr 1 X 2 3 Dx 雨露学习互助

Integral Of 1 X 2 X Partial Fraction Decomposition Youtube

怎麼求1 X X 3 的積分 人人焦點

How Do You Integrate E 3x Sin 2x Dx Socratic

How Do You Evaluate Int 0 1 Sqrt X X 2 Dx Socratic

1 X 2 A 2 Dxの計算 物理のかぎしっぽ

Incoming Term: 1/1+x^2 積分 無限, 1/1+x^2 積分 アークタンジェント, 1/1+x^2 積分 tan, 1/1+x^2 積分 複素, 1/1+x^2 積分 大学, 1/1-x^2 積分 tanh, 1/1+x^2 積分 公式, 1/1+x^2 積分 log, 1/1+x^2 積分, y=1/1+x^2 積分,